[JAVA] 3085번 - 사탕게임
문제 탐색하기
- 문제에서 구해야 하는 최종 정답은 무엇인지 탐색한 과정
- 그 정답을 구하기 위해 어떻게 코드를 구현해야 할지 고민한 과정
- 문제에 들어오는 범위를 파악하여 어떤 알고리즘을 쓸 수 있을지 고민해 가는 과정
해결방법 추론
서로 다른 인접한 사탕 두개를 교환하고, 한번 교환할때마다 보드판을 전부 탐색해서 가장 긴 연속 부분을 찾아서 최댓값으로 계속 업데이트 시켜줘야한다. 이걸 보드판을 탐색하면서 서로 다른 인접할 사탕이 있을때마다 해야한다.
그런데 서로 다른 인접한 사탕이 가로로 있을수도 있고, 세로로 있을 수도 있다. 그래서 가로,세로 모두 교환해줘야한다.
여기서 든 생각은 이렇다.
for문으로 모든 보드판을 탐색해야하는데, 그럼 하나의 좌표 기준으로, 오른쪽에 있는 사탕, 밑에 있는 사탕 이렇게만 고려하면 된다.
보드판을 순회하며 파란색 좌표c의 차례가 되었을때, 위쪽, 왼쪽은 고려하지 않아도 된다. 이전의 빨간색동그라미 좌표를 순회할때 이미 오른쪽, 밑을 교환해서 체크했을것이기 때문이다.
그래서 본인 좌표 기준 오른쪽사탕, 밑사탕을 교환하는 경우만 고려하면된다.
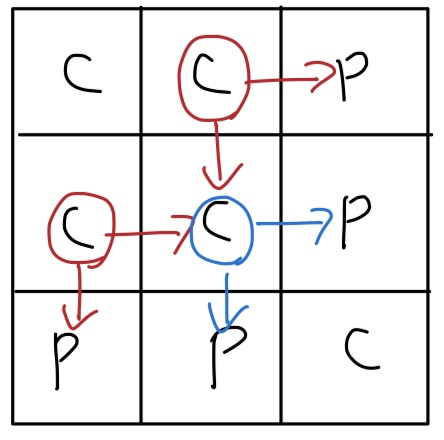
이걸 생각하면 문제를 풀어야하는 알고리즘은 거의 다 해결된 것같다.
이걸 생각하기 전에는 for문 돌면서 서로 다른거 교환하고, 그걸 방문처리를 하고, 가장긴부분체크하고, 다시 for문 돌면서 방문하지 않은 사탕들 가로로 교환하고 해야하나 생각했었다
시간복잡도
n은 최대 50이고 이중for문을 돌아야하니까 O(2500)이다 1초안에 충분히 가능하다.
시뮬레이션 설계
1.이중for문으로 보드판을 순회한다
2-1) 서로 인접한 가로
①서로 인접한 가로의 사탕을 교환한다
②교환한 상태에서 가장 긴 연속 부분을 업데이트한다
③다음 탐색을 위해 교환했던걸 원상복귀한다.
2-2) 서로 인접한 세로
①서로 인접한 세로의 사탕을 교환한다
②교환한 상태에서 가장 긴 연속 부분을 업데이트한다
③다음 탐색을 위해 교환했던걸 원상복귀한다.
코드 설계하기
위의 문제 탐색하기에서 고민한 과정을 토대로 문제 풀이에 대한 실마리를 잡았다면, 문제 풀이를 본격적으로 하기전, 문제를 풀이 위한 로드맵을 그려본다
어떤 순서로 코드를 작성해야 할지, 어떤 함수들을 작성해야 할지 등을 작성
1. 사탕위치 교환
가로일때, 세로일때로 분기하여 코드를 짰다.
범위를 체크할때 오른쪽 사탕, 밑사탕의 범위가 넘어가지 않는지도 체크해야한다!
// 서로 인접한 가로 두칸 교환
for(int i=0; i<n-1; i++) {
for(int j=0; j<n-1; j++) {
// 서로 인접한 가로 교환
if(board[i][j] != board[i][j+1] && j+1<n) {
char tmp = board[i][j];
board[i][j] = board[i][j+1];
board[i][j+1] = tmp;
// 모두 같은 색으로 이루어진 가장 긴 연속 부분 고름
ans = Math.max(ans, checkMaxNum());
//원상복귀
char tmp1 = board[i][j];
board[i][j] = board[i][j+1];
board[i][j+1] = tmp1;
}
// 서로 인접한 세로 교환
if(board[i][j] != board[i+1][j] && i+1<n) {
char tmp = board[i][j];
board[i][j] = board[i+1][j];
board[i+1][j] = tmp;
ans = Math.max(ans, checkMaxNum());
char tmp2 = board[i][j];
board[i][j] = board[i+1][j];
board[i+1][j] = tmp2;
}
}
2. 가장 긴 연속 부분 고르기
보드판을 순회하면서 가장 긴 연속 부분을 찾아야한다.
가로일때 가장 긴연속부분, 세로일때를 나눠서 각각 찾아준다.
private static int checkMaxNum() {
int max_cnt = 1;
for(int i=0; i<n; i++) {
int cnt=1;
for(int j=1; j<n; j++) {
if(board[i][j]==board[i][j-1]) {
cnt++;
}
else {
cnt=1;
}
max_cnt = Math.max(cnt, max_cnt);
}
for(int j=1; j<n; j++) {
if(board[j][i] == board[j-1][i]) {
cnt++;
}
else {
cnt=1;
}
max_cnt = Math.max(cnt, max_cnt);
}
}
return max_cnt;
}
시도 회차 수정 사항
- 무분별하게 "맞았습니다" 가 나올때까지 수정하는 형태의 문제 풀이를 반복하면, 내가 어떤 실수를 해서 해당 문제를 틀렸는지 모르게 된다
- 틀렸습니다를 받았다면 왜 틀렸는지 고민핸보고, 어떻게 수정할 수 있는지 고민하는 과정을 작성
- 위에 내가 세울 설계에서 어떤 부분이 틀렸는지도 함께 점검
import java.io.*;
import java.util.*;
public class Main {
static int n;
static char [][]board;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
board = new char[n][n];
for(int i=0; i<n; i++) {
String line = br.readLine();
for(int j=0; j<n; j++) {
board[i][j] = line.charAt(j);
}
}
int ans = 1;
// 서로 인접한 가로 두칸 교환
for(int i=0; i<n-1; i++) {
for(int j=0; j<n-1; j++) {
// 서로 인접한 가로 교환
if(board[i][j] != board[i][j+1] && j+1<n) {
char tmp = board[i][j];
board[i][j] = board[i][j+1];
board[i][j+1] = tmp;
// 모두 같은 색으로 이루어진 가장 긴 연속 부분 고름
ans = Math.max(ans, checkMaxNum());
//원상복귀
char tmp1 = board[i][j];
board[i][j] = board[i][j+1];
board[i][j+1] = tmp1;
}
// 서로 인접한 세로 교환
if(board[i][j] != board[i+1][j] && i+1<n) {
char tmp = board[i][j];
board[i][j] = board[i+1][j];
board[i+1][j] = tmp;
ans = Math.max(ans, checkMaxNum());
char tmp2 = board[i][j];
board[i][j] = board[i+1][j];
board[i+1][j] = tmp2;
}
}
}
System.out.println(ans);
}
private static int checkMaxNum() {
int max_cnt = 1;
for(int i=0; i<n; i++) {
int cnt=1;
for(int j=1; j<n; j++) {
if(board[i][j]==board[i][j-1]) {
cnt++;
}
else {
cnt=1;
}
max_cnt = Math.max(cnt, max_cnt);
}
for(int j=1; j<n; j++) {
if(board[j][i] == board[j-1][i]) {
cnt++;
}
else {
cnt=1;
}
max_cnt = Math.max(cnt, max_cnt);
}
}
return max_cnt;
}
}